Mesh Simplification using Quadric Error Metrics

This time, I’ve done a quick and short research on mesh simplification algorithm (and homogeneous coordiantes, quadrics) using quadric error metrics (and planning on implementing this algorithm with Unity Engine). Be aware that not all of this information may be correct.

Homogeneous coordinates (projective coordinates)

railroad; source: https://www.songho.ca/math/homogeneous/homogeneous.html

In contrast to Euclidean geometry (three-dimensional space), projective geometry introduces another Z dimension, called W, in which it is used to describe the distance from the projector to the screen.

In order to correctly convert a 3D coordinate into a 4D coordinate without modifying any property, one should always set W = 1. Doing this has no effect on the X, Y or Z values. In other words, if one renders coordinates with W > 1, everything would look small; W < 1 everything would look too big. Furthermore W = 0 would result in a divide by zero error.

Despite it being 4D vectors similar to quaternions, homogeneous coordinates have different concepts with different use cases. In much simpler terms: two parallel lines can intersect each other in projective space (seen from the railroad model).

In computer graphics, utilizing homogeneous coordinates allows common operations such as translation (“move”), rotation and scaling.

Quadrics

Quadrics are defined by quadratic equations (second-degree equations) in two dimensional spaces and many common shapes (e.g. spheres, ellipsoids, tori, paraboloids and hyperboloids) can be modeled with quadrics. E.g. spheres generally have a quadratic equation of: x2 + y2 + z2 = rz

Surface simplification general goals

By simplifying a mesh, it allows for an implementation of various LODs (level of details) in computer graphics. The ultimate goal in doing this is to preserve computing resources, as such complex models are not always required to display adequate level of realism. Albeit the simplification may occur, the quality of a simplified mesh should not differ too much from the original source, as the primary goal in computer graphics application is to maintain a convincing level of realism most of the time. This process should be done by taking a polygonal model as input and generate a simplified model as output.

In 3D graphics, 3 dimensional models or meshes / polygon meshes consist of vertices, edges and faces. The achievement should be to have less vertices / edges / faces.

Edge contraction

Iterative edge contraction is an algorithm, in which it stands for the foundation for quadric error metrics surface simplification. The idea of this algorithm is to take a pair of vertices (v1 and v2; edge) and contract to just one single vertex. Non-edge contractions will join non-edge pairs together. This operator, however, may result in concerning topology results (e.g. unacceptable fragmentation). The matter isn’t as significant in applications such as rendering. Other relevant algorithms include: vertex decimation and vertex clustering.

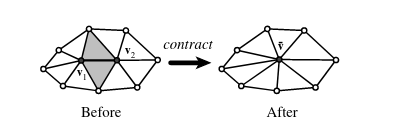
Optimal pair selection In order to apply an iterative edge contraction algorithm appropriately, a valid vertex pair must be selected. A pair (v1, v2) is a valid pair for contraction if either:

(v1, v2) is an edge or
||v1 - v2|| < t, where t is a threshold parameter

If t = 0, then only the actual edges of the mesh will be selected as a valid pair. Higher thresholds allow non-connected vertices to be paired.

Quadric error

In order to perform the contraction to a selected optimal pair, an optimal position of the vertex must also be determined. Defined is “overall error” between M0 (input mesh) and Mr (resulting mesh; simplified mesh) as a function of 𝚫(v). A simple scheme to locate the best position is to select either the positions of v1, v2 or (v1 - v2)/2, depending on which one of these produces the lowest value of 𝚫(v). Although, finding a position of vertex with the minimum value of 𝚫(v) is most ideal.

Measuring error with quadrics

Meshes consist of triangles (three vertices make up to a triangle); One vertex v1 can be associated with many triangles. These triangles can be expressed as a plane. By using cross products, the normal vector of this plane can be calculated, ergo the plane equation. The plane equation is ax + by + cz + d = 0 where a2 + b2 + c2 = 1 (normalized normal vector). Measurement of error with quadrics can be done by computing the sum of squared distance of a vertex v1 to its associated planes. This can be interpreted as 4x4 matrix multiplication (with v1 being a homogeneous vector (x, y, z, 1); w component/Euclidian distance) = 1). Optimal position for v can be calculated based on the minimal value of this measurement (which would also result in a minimal value of 𝚫(v)).

One can stop the algorithm once the mesh has reached a certain amount of vertex count.

With that being said, I’m still not entirely certain about the math behind the entire algorithm.

Read more about the algorithm here: https://www.cs.cmu.edu/~./garland/Papers/quadrics.pdf

Now here’s the implementation in Unity: WIP